Content
Great circle distance between places with the same latitude
Finding the great circle distance between two places on the same latitude takes advantage of the fact that both places are on the circumference of the same small circle.
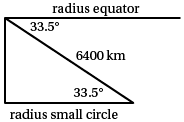
Knowing the radius of that small circle and the angle between the small circle radii to each place (from the difference in longitudes), we can calculate the straight line distance between the two places using the cosine rule. Then using this distance and the radius of the earth (6400 km), we can again use the cosine rule, this time to calculate the angle between the two earth radii to each place.
(This angle will be different to the difference in longitudes due to the curvature of the earth - the closer to the poles we go, the greater the difference between this angle and the difference in longitudes.)
Finally, using this angle and the radius of the earth, we can calculate the great circle distance.
Example
Both Sydney (Australia) and Cape Town (South Africa) are on the ${33.5^{\circ}}$ S parallel of latitude, but Sydney is at ${151.13^{\circ}}$ E whereas Cape Town is at ${18.22^{\circ}}$ E. How far is it from Sydney to Cape Town travelling the great circle route, correct to the nearest km?
Solution
For the small circle,
$\begin{aligned}[t] &r =6400\times \cos 33.5^{\circ}\\ &=5336.869\ldots \\ &\approx 5337\text{ km} \end{aligned}$Longitude angle difference for Sydney and Cape Town is ${151.13^{\circ}} - {18.22^{\circ}} = {132.91^{\circ}}$.

Straight line distance from Sydney to Capetown
$\begin{aligned} d& = \sqrt{5337^2 + 5337^2 - 2 \times 5337 \times 5337 \times \text{ cos} 132.91^{\circ}}\\ & = 9785 \text{ km} \end{aligned}$Angle between earth radii
$\begin{aligned} \theta& = \cos^{-1} \left(\frac{6400^2 + 6400^2 - 9785^2}{2 \times 6400 \times 6400}\right)\\ & = 99.72^{\circ} \end{aligned}$
From Sydney to Cape Town via great circle route
$\begin{aligned} &=\frac{r\pi}{180^{\circ}}\times\theta\\ & =\frac{6400\pi}{180^{\circ}}\times 99.72^{\circ}\\ & =11138.831\ldots \approx 11139\text{ km} \end{aligned}$We can see that, compared to the distance around the ${33.5^{\circ}}$ parallel of latitude which was 12380 km, the great circle route at 11139 km is some 1241 km shorter.
Example
Both Launceston (Tasmania, Australia) and Puerto Monti (Chile, South America) are on the ${41.3^{\circ}}$ S parallel of latitude, but Launceston is at ${147.08^{\circ}}$ E whereas Puerto Monti is at ${72.57^{\circ}}$ W. How far is it from Launceston to Puerto Monti travelling the great circle route, correct to the nearest km?
Solution

For the small circle,
$\begin{aligned}[t] r & =6400\times \cos {41.3^{\circ}}\\ & =4808.090\ldots \\ &\approx 4808\text{ km} \end{aligned}$The angle between the longitude of Launceston and that of Puerto Monti is ${147.08^{\circ}} + {72.57^{\circ}} = {219.65^{\circ}}$. We find the sum since these places are on different sides of the Prime Meridian, but this is the major arc, and the minor arc will be ${360^{\circ}} - {219.65^{\circ}} = {140.35^{\circ}}$.

Straight line distance from Launceston to Puerto Monti
$\begin{aligned}[t] d& = \sqrt{4808^2 + 4808^2 - 2 \times 4808 \times 4808 \times \text{ cos} 140.35^{\circ}} \\ & = 9046 \text{ km} \end{aligned}$Angle between earth radii
$$ \theta = \cos^{-1} \left(\frac{6400^2 + 6400^2 - 9046^2}{2 \times 6400 \times 6400}\right) = 89.94^{\circ}$$
From Launceston to Puerto Monti via great circle route
$\begin{aligned}[t] &=\frac{r\pi}{180^{\circ}}\times\theta\\ & =\frac{6400\pi}{180^{\circ}}\times 89.94^{\circ} \\ &=10046.394\ldots &\approx 10046\text{ km} \end{aligned}$
We can see that, compared to the distance around the ${41.3^{\circ}}$ parallel of latitude which was 11778 km, the great circle route at 10046 km is some 1732 km shorter.
